10. Errors
Errors
SOLUTION:
- Distance of vehicle from trajectory.
- Difference of vehicle orientation and trajectory orientation.
We can capture how the errors we are interested in change over time by deriving our kinematic model around these errors as our new state vector.
The new state is [x, y, \psi, v, cte, e\psi] .
Let’s assume the vehicle is traveling down a straight road and the longitudinal direction is the same as the x-axis.
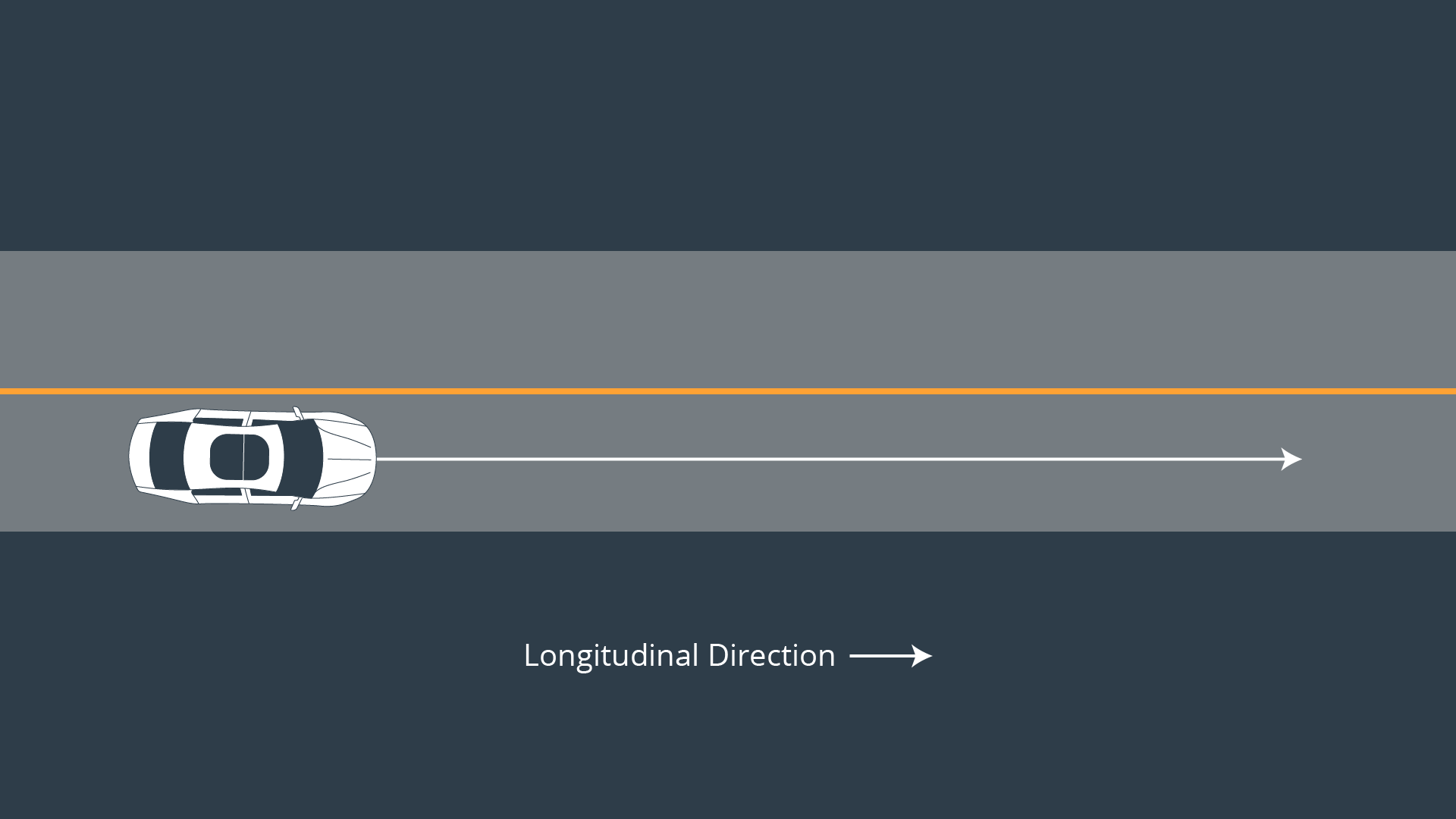
Cross Track Error
We can express the error between the center of the road and the vehicle's position as the cross track error (CTE). The CTE of the successor state after time t is the state at t + 1, and is defined as:
cte_{t+1} = cte_t + v_t* sin(e\psi_t) * dt
In this case cte_t can be expressed as the difference between the line and the current vehicle position y . Assuming the reference line is a 1st order polynomial f , f(x_t) is our reference line and our CTE at the current state is defined as:
cte_t = f(x_t) - y_t
If we substitute cte_t back into the original equation the result is:
cte_{t+1} = f(x_t) - y_t + (v_t * sin(e\psi_t) * dt)
This can be broken up into two parts:
- f(x_t) - y_t being current cross track error.
- v_t * sin(e\psi_t) * dt being the change in error caused by the vehicle's movement.
Orientation Error
Ok, now let’s take a look at the orientation error:
The update rule is essentially the same as \psi .
e\psi_t is the desired orientation subtracted from the current orientation:
We already know \psi_t , because it’s part of our state. We don’t yet know \psi{des}_t (desired psi) - all we have so far is a polynomial to follow. \psi{des}_t can be calculated as the tangential angle of the polynomial f evaluated at x_t , arctan(f'(x_t)) . f' is the derivative of the polynomial.
Similarly to the cross track error this can be interpreted as two parts:
- \psi_t - \psi{des}_t being current orientation error.
- \frac{v_t} { L_f} * \delta_t * dt being the change in error caused by the vehicle's movement.
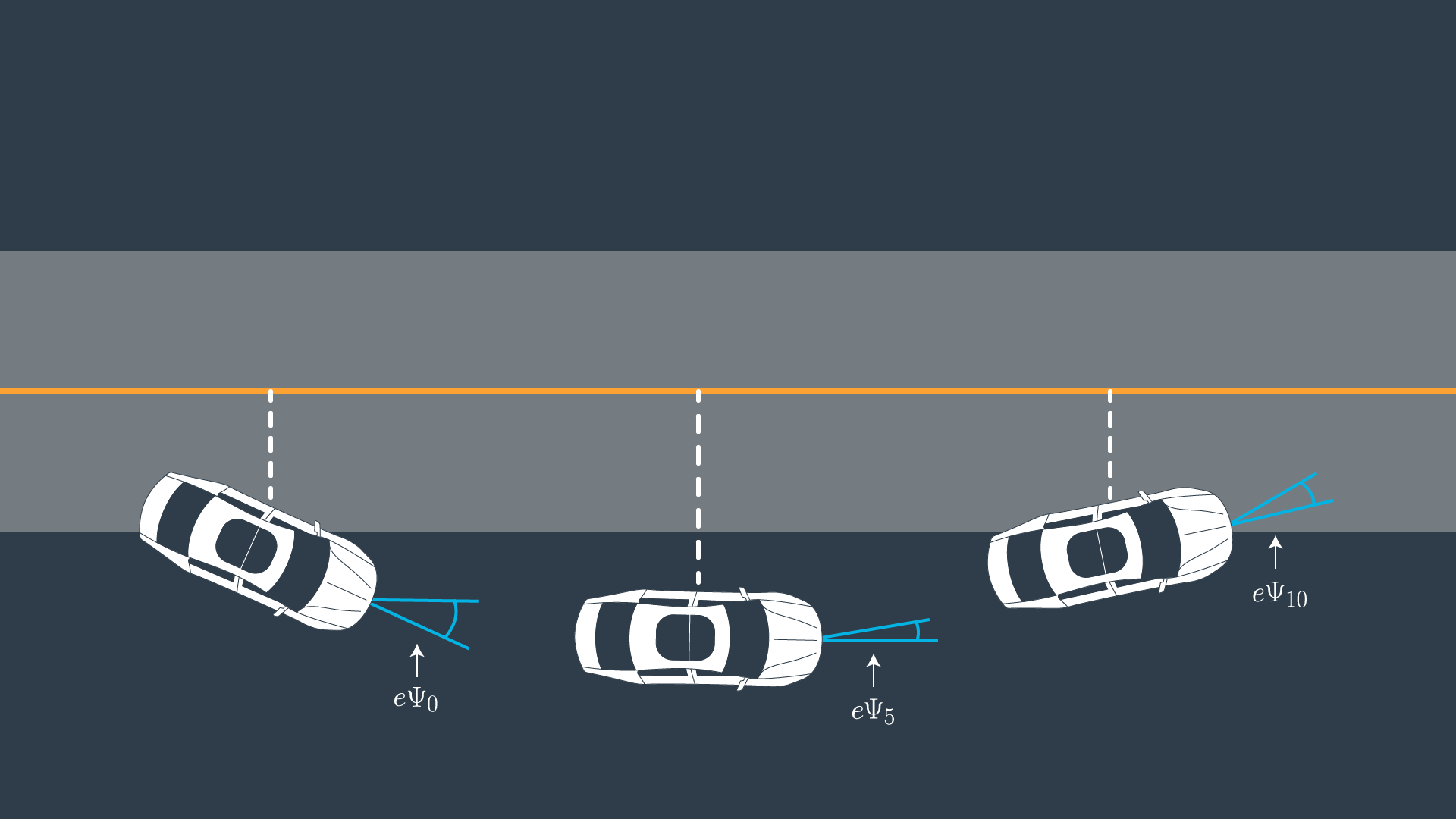
The dashed white line is the cross track error.